- Синус проти прямих
- неминуча окружність
- Рубрика «Питання і відповіді»
- π без картинок
- Наскільки швидкий синус?
- Частина 2: Розуміння визначень синуса
- Визначення 1: Висота трикутника / окружності!
- Визначення 2: Нескінченний ряд
- Покопаємось в розрахунках
- обчислення косинуса
- Визначення 3: Диференціальне рівняння
- Підсумуємо
Синусоїди завжди мене бентежили. Можна нескінченно малювати трикутники і повторювати теореми напам'ять. Але що вони означають?
Я зайшов в глухий кут, намагаючись витягти синус з інших форм. Швидка аналогія:
Ви: Геометрія описує форми, лінії і т.д.
Прибулець: Невже? А покажи мені лінію.
Ви (оглядаючись на всі боки): Мм ... бачиш отой цегла? Лінія - це один з його торців.
Прибулець: Тобто лінія - це частина фігури?
Ви: На зразок того. Так, більшість фігур складаються з ліній. Але лінія - це сам по собі базовий концепт: промінь світла, прямий маршрут на карті, або навіть вектор у багатьох вимірах. Розумієш?
Прибулець: Лінії походять від цегли. Цеглини, цеглини, цеглини ...
Бачите? Ось тому, що синус постійно показують за допомогою кутів і кіл, мій мозок думає: «Синус стався від кіл. Кола, кола, кола ».
Все досить. Ось так буде правильніше: Синус - це природне коливання, втілення гладкості: він робить окружності «округлими» таким же чином, як прямі роблять квадрати «квадратами».
Давайте будемо будувати наше уявлення про синусе як про окрему фігурі, і потім зрозуміємо, як він вбудовується в окружності і так далі. Вперед!
Синус проти прямих
Не забувайте розділяти ідеї і приклади: квадрат - це лише приклад поєднання ліній. А синус як поняття зовсім не є «частиною окружності».
Давайте розглянемо синус в симуляторі.
Смайлик почне свій шлях:
- Натисніть start. Давай, смайлик, біжи! Помітили це плавний рух вперед-назад? Цей смайлик і є синус. У такому ж стилі вібруютьструни, стискаються і розтискаються пружини, обертається маятник ... і ще дуже багато різних тел рухаються.
- Змініть «vertical» на «linear». Велика різниця - бачите, якими різкими стали руху на краях амплітуди?
Давайте розглянемо відмінності на відео:
- Рух linear постійно: ми рухаємося з постійною швидкістю і різко міняємо напрям. Це неприродне рух, як танцюють в стилі «робот» (на 0:07 руху танцюриста дуже плавні, а на 00:38 він показує вже стробоскопічний ефект).
- Синус змінює свою швидкість: починає рухатися швидко, сповільнюється, зупиняється, а потім знову прискорюється. Ох вже ці чарівні переходи в танці! (На 0:12 і 0:23 можна побачити справжню людську синусоїду, а на 00:47 - природна пружність).
На жаль, в підручниках танці не показують як приклад синусоїди. Авторам більше подобається представляти синусоїду змінюється в часі (встановіть «horizontal» в графі «timeline»):
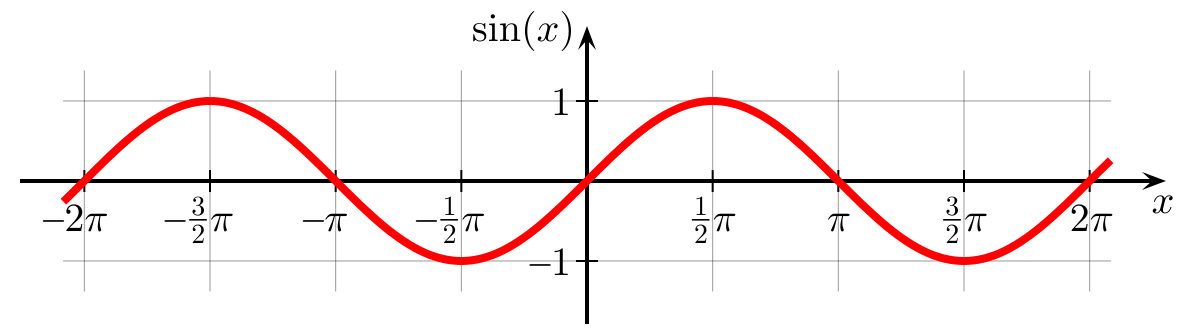
( вікіпедія )
Прокляття. Ось цей схематичний графік нам завжди і показували. Ви по ньому уявляєте, що таке синус? Приблизно так само, як якщо б вас змусили уявити спритність кота по зображенню його скелета. Давайте спочатку вивчимо синус в русі, а потім, звичайно, зобразимо його на графіку.
неминуча окружність
У окружності є синус. Так. Але побачити синус всередині кола - це все одно, що отримати з омлету яйця назад, коли всі вони гарненько один з одним перемішані!
Давайте повільніше. У симуляторі встановіть такі параметри: vertical: none і horizontal: sine *. Бачите, як смайлик рухається вперед-назад? Це і є рух синуса. Невеликий фокус: зазвичай синус починає свій цикл на нейтральній серединної точці і біжить до максимуму. На цей раз ми починаємо в максимумі і падаємо до серединної точці. Синус, який «стартує на максимумі», називається косинусом, і це просто версія синуса (як горизонтальна пряма є версією вертикальної прямої)
Настав час для обох синусних хвиль: встановіть параметри vertical: sine і horizontal: sine *. І ... у нас вийшла окружність!
Горизонтальні і вертикальні «стрибки» в сумі дали круговий рух. У більшості підручників малюють коло і намагаються витягти з неї синус, але я віддаю перевагу зворотний підхід: розпочати з простого горизонтального або вертикального руху і додати протилежне.
Рубрика «Питання і відповіді»
Перший раз, вивчаючи синуси, я упустив кілька речей:
Синус взагалі-то 1-мірний.
Синус рухається в одному вимірі. Правда. Ми часто малюємо синус, що змінюється в часі, а іноді і «предмет», що описує своїм рухом синус, теж кудись рухається, але це вже опціонально! Стрибок в одному напрямку - цілком собі повноцінна хвиля синусоїди.
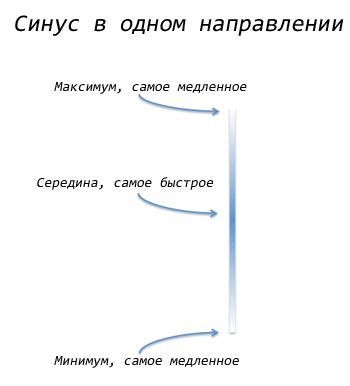
Кола - це приклад синусних хвиль.
Кола і квадрати - це комбінації базових елементів (синусів і прямих відрізків). Але окружності не є основою синусоїди, як і квадрат не є складовою частиною прямої.
Що показують значення синуса?
Синус приймає значення від -1 до 1. Він починається з 0, зростає до 1.0 (максимум), падає до -1.0 (мінімум) і знову повертається в нейтральну точку, до нуля. Я також бачу синус як відсоток від 100% (повний вперед!) До -100% (повний зворотний хід).
Що означає вступне значення 'x' у функції sin (x)?
Каверзне питання. Оскільки це цикл і х - вступний параметр, він означає, як далеко ми пройшли по колу.
Розглянемо приклад з лініями:
- Ми блукаємо по квадрату. За 10 секунд ми проходимо кожну сторону.
- Через 1 секунду, ви пройшли 10% від однієї сторони
- Через 5 секунд, ви пройшли одну сторону на 50%
- Через 10 секунд ви пройдете всю сторону.
У лінійному русі є парочка сюрпризів. Розглянемо тепер синус (сфокусуємось на циклі «від 0 до максимуму»):
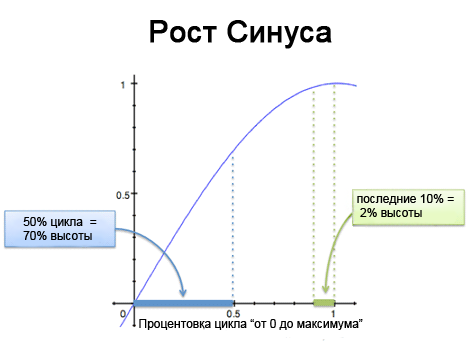
- Ми подорожуємо по синусоїді, стартуючи з 0 (нейтральна точка) до 1.0 (максимум). І на цей шлях у нас пішло 10 секунд.
- Через 5 секунд ми ... пройшли 70%! Синус дуже швидкий на старті, і потихеньку сповільнюється до вершини. Так що більшу частину шляху ми пройдемо за перші 5 секунд.
- І ще 5 секунд нам буде потрібно на те, щоб пройти з 70% до 100% шляху. А відрізок з 98% до 100% займає майже цілу секунду!
Незважаючи на високу початкову швидкість, синус уповільнює своє зростання, так що ми дуже плавно торкаємося точки максимуму і повертаємося назад. Ця плавність і робить синус синусом.
Якщо вам дуже цікаві подробиці, натисніть «show stats» в симуляторі. Ви побачите відсоток виконання повного циклу, міні-циклу (з 0 до 1.0) і поточне значення. Зупиніть рух (кнопка Stop), попереключать між лінійним і синусоїдальним рухом, щоб порівняти значення.
Маленька перевірка: Що буде далі, 10% лінійного циклу або 10% синусового? Правильна відповідь - синусового.
Пам'ятайте, на самому початку синус максимально прискорений. На час досягнення 50% циклу, синус рухається із середньою швидкістю лінійного циклу і, більш того, сповільнюється (поки не досягне максимуму і не розвернеться).
Так що x - це «кількість вашого циклу». Якого циклу?
Залежить від контексту.
- Базовий варіант: 'x' - це градуси, і повний цикл складається з 360 градусів
- Високий рівень варіант: 'x' - це радіани ( вони більш натуральні! ) І повний цикл складає повний прохід по одиничному колі (2 * π радіан)
Експериментуйте зі значенням х тут:
Але знову ж таки, цикли залежать від кіл! Чи можемо ми якось вирватися з-під їх тиранії?
π без картинок
Уявіть собі сліпого прибульця, який може розрізняти тільки тіні світла і темряви. Чи можете ви пояснити йому, що таке π? Досить складно пояснити в такій ситуації поняття довжини окружності, вірно?
Давайте повернемося трохи назад. Синус - це циклічна функція. Це означає, що значить її значення повинні ... повторюватися! Синус починається з 0, йде до 1, до 0, до -1, до 0 і так далі.
Давайте визначимо π як час, за яке синус піднімається з 0 до 1, і назад повертається до 0. Вау! Тепер і ми використовуємо π без всяких кіл!
- Синус - це плавне пересування вперед-назад
- π - це час руху синуса з 0 до 1 і назад до 0
- n * π (0 * π, 1 * π, 2 * π і т.д.) - це момент часу, в якому синус дорівнює 0
- 2 * π, 4 * π, 6 * π і т.д. - повні періоди синуса.
Ага! Ось чому π зустрічається в такій кількості формул! π не "належить" колах більше, ніж 0 або 1 - π стосується повернення синуса в центр! Окружність - це приклад фігури, яка повторюється і повертається в центр кожні 2 * π одиниць. Але вібрації, скачки і т.д. повертаються до центру кожен π!
Питання: якщо π - це половина природного періоду, чому воно триває вічно (є ірраціональним числом)?
Можна я відповім питанням на питання, А чому довжина діагоналі «одиничному колі» дорівнює квадратному кореню з 2, який також йде в нескінченність?
Але так, я розумію, що це філософськи не зручно , Коли природа поводиться довільно. Але що поробиш ...
Наскільки швидкий синус?
Я вас трохи заплутав. Спочатку я сказав: «уявіть, що синусу потрібно 10 секунд, щоб дістатися з 0 до максимуму». А зараз я говорю, що йому треба π секунд, щоб дістатися з 0 до максимуму і назад спуститися до 0. Що відбувається?
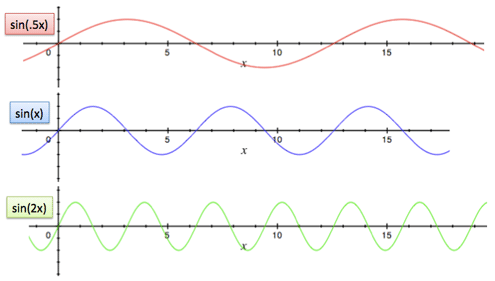
- sin (x) - це базова синусная хвиля, якої дійсно потрібно π одиниць часу, щоб пройти шлях з 0 до максимуму і знову до 0 (або 2 * π, щоб обійти свій повний період)
- sin (2x) - це синусоїда, яка рухається вдвічі швидше
- sin (x / 2) - це синусоїда, яка рухається вдвічі повільніше базової
Так що ми використовуємо sin (n * x), щоб зробити синус, який буде рухатися так швидко, як нам потрібно. Дуже часто слово «синусоїда» використовується для вказівки загальної форми хвилі, а не конкретної швидкості.
Частина 2: Розуміння визначень синуса
Це складно - так що зробіть перерву, наберіться сил. Сподіваюся, скоро в нашій свідомості вималюється синус як окреме поняття. Давайте знайдемо зв'язок між звичними визначеннями синуса.
Визначення 1: Висота трикутника / окружності!
Синус вперше знайшли в трикутнику.
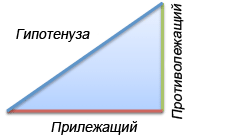
- Синус - це відношення протилежного катета до гіпотенузи
- Косинус - це відношення прилеглого катета до гіпотенузи
- Тангенс - це співвідношення між протилежним і прилеглим катетами
Для прямокутного трикутника з кутом х, sin (x) - це довжина протилежного катета, поділена на довжину гіпотенузи. Якщо ми візьмемо гіпотенузи, що дорівнює 1, то це визначення можна спростити до:
- Синус = протилежного катета
- Косинус = прилеглого катета
А з великим розумом, ми можемо намалювати трикутник з гіпотенузою 1 в окружності з радіусом 1:
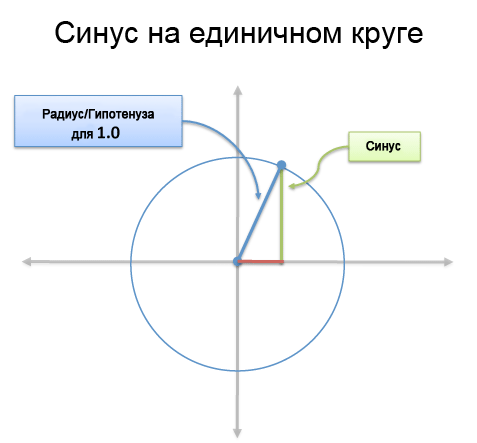
Вуаля! Окружність, що містить всі можливі прямокутні трикутники (оскільки розмір трикутника з одиничному колі можна масштабувати до будь-якого розміру). наприклад:
- sin (45) = 0.707
- Візьміть 10-метровий стовп і підійміть його з землі на 45 градусів. Верхівка стовпа буде 10 * sin (45) = 7.07 метрів від землі
- А 8-метровий стовп буде 8 * sin (45) = 5.65 метрів від землі
Подібні маніпуляції зі стовпами дуже корисні в будівництві (піраміди самі себе не розрахують). На жаль, через тисячі років у нас твердо закріпилася думка, що сенс синуса в неможливо розрахувати висоту трикутника по гіпотенузі і розі. Ні і ще раз ні, синус - це форма, яку можна виявити в колах (і трикутниках). У реальності, ми часто переходимо в «режим геометрії» і для стислості розумового процесу думаємо «синус = висота». Це нормально, головне не застрявати на цьому, а дивитися ширше.
Визначення 2: Нескінченний ряд
Я сховав слона в кімнаті: як ми взагалі обчислюємо синус? Мій калькулятор, що, кожен раз малює окружність і заміряє його?
Радий вам розповісти, як можна обчислити синус без околиць.
Синус - це прискорення в сторону, протилежну тому, де ви знаходитесь.
Користуючись нашим прикладом з банківським рахунком : Уявіть, що ваш шеф щотижня вирішив міняти вашу зарплату на суму, протилежну поточної на вашому банківському рахунку. Якщо у вас зараз є 50 рублів, на наступному тижні шеф видасть на 50 рублів менше. Звичайно, оскільки ваш дохід буде 75 рублів, ви все ще будете в плюсі (75 - 50) але в підсумку ваш баланс зменшиться, оскільки «добавки» шефа перевершать ваші доходи.
Але не впадайте у відчай! Як тільки баланс стає негативним (скажімо, у вас -50 рублів), ваш бос видасть вам на цілих 50 рублів більше. Потім знову баланс стане негативним (з його зростанням шеф видає все менше грошей), і так буде тривати постійно. Баланс буде то позитивний, то нульовий, то негативний.
Цей приклад також пояснює, чому в нейтральній точці (в 0) швидкість синуса максимальна: коли ви на максимумі, ви починаєте падати і збирати все більше «негативних збільшень», які досить швидко тягнуть вас до 0. Після проходження 0 ви починаєте отримувати найбільш значні позитивні надбавки і сповільнюється., тому що як тільки йдіть в плюс, шеф знову починає забирати від вашої зарплати.
Між іншим: оскільки синус - це прискорення, зворотне до вашого поточного місцезнаходження, а окружність зроблена з горизонтальною і вертикальною синусоїди ... ви зрозуміли! Круговий рух може бути описано як «постійний рух в напрямку, протилежному поточної позиції, у напрямку до горизонтального і вертикального центру».
Покопаємось в розрахунках
Давайте опишемо синус за допомогою обчислень. Як у випадку з e, ми можемо розбити синус на маленькі частини:
- Почнемо з 0 і доростемо до одиничної швидкості
- У кожен момент часу ми будемо сповільнюватися через негативного прискорення
І як про все це думати? Подивіться, як кожна наша дія змінює відстань від центру:
Розуміння того, як прискорення впливає на відстань, схоже на спостереження за тим, як надбавки впливають на ваш банківський рахунок. «Збільшення» повинна змінювати ваш дохід, а ваш дохід змінює стан вашого банківського рахунку (два інтеграла «по команді»).
Так що після «х» секунд, ми вже здогадаємося, що синус це «х» (початковий імпульс) мінус x ^ 3/3! (Ефект прискорення):
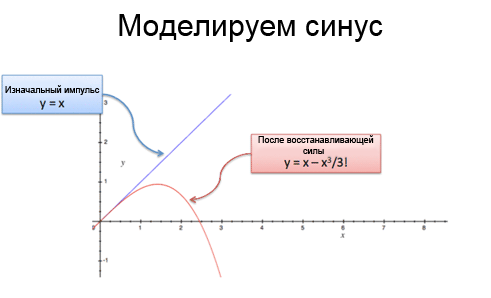
Щось не так - синус не спадає! У випадку з е ми бачили, що «відсотки приносять свої відсотки», у випадку з синусом відбувається те ж саме. «Повертається сила» змінює наше відстань на -x ^ 3/3 !, що створює іншу повертає силу. Розгляньте пружину: якщо відпустити пружину з грузиком внизу, то поштовх буде досить великим, щоб створити інший поштовх, який потягне грузик назад вгору, а потім знову вниз. Ох вже ці невгамовні пружини!
Нам потрібно розглянути кожну повертає силу:
- y = x - це наше початкове рух, яке створює повертає силу удару:
- y = -x ^ 3/3 !, яка створює повертає силу удару:
- y = x ^ 5/5 !, яка створює повертає силу удару:
- y = -x ^ 7/7 !, яка створює повертає силу удару ...
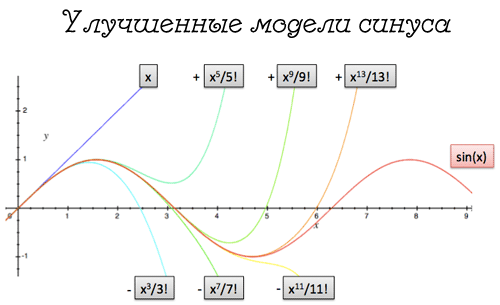
Точь-в-точь як е, синус можна описати нескінченним рівнянням:
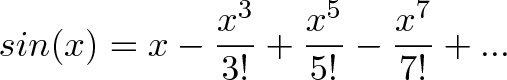
Я бачив цю формулу багато разів, але до мене дійшов її сенс тільки коли я представив синус як комбінацію початкового імпульсу і повертають сил. Початковий імпульс (y = x, росте вгору) в результаті перевершує повертає сила (яка штовхає нас вниз), і ця сила в свою чергу поступово компенсується своєї повертає силою (що знову штовхає нас вгору), і так далі.
Пара цікавих заміток:
- Розглядайте «повертає силу» як «позитивний або негативний відсоток». Так простіше зрозуміти зв'язок синуса і е у формулі Ейлера. Синус поводиться як е, крім моментів, коли він починає заробляти негативний відсоток. Тут нам ще треба повчитися :).
- Для маленьких чисел «y = x» - непогане припущення для синуса. Ми просто беремо початковий імпульс і ігноруємо повертають сили.
обчислення косинуса
Косинус - це просто зміщений синус, і дуже добре, що тепер нам з синусом все ясно:
- Синус: починається з 0, початковий імпульс y = x (100%)
- Косинус: починається з 1, ніякого початкового імпульсу немає
Косинус просто починає ... сидить на 1. Ми запускаємо в роботу повертає силу:
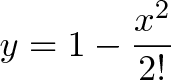
Знову ж таки, ми інтегруємо -1 двічі, щоб отримати -x ^ 2/2 !. Але це провокує іншу повертає силу, і ось що в підсумку виходить:
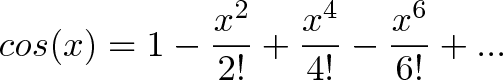
Визначення 3: Диференціальне рівняння
Ми описали поведінку синуса певними рівняннями. Коротенько це буде виглядати так:
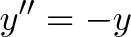
Ця краса означає наступне:
- Наша поточна позиція - y
- Наше прискорення (2-я похідна, або у ") - назад нашої поточної позиції (-y)
Це справедливо і для синуса, і для косинуса. Спочатку я просто ненавидів це визначення; воно таке несхоже на нашу візуалізацію. Я не розумів, що воно описувало суть синуса: «прискорення, зворотне поточної позиції».
І згадайте як синус і е пов'язані? Ну, e ^ x можна описати рівнянням:

Те ж рівняння з позитивним знаком ( «прискорення дорівнює поточної позиції»)! Коли синус - це «висота кола», дуже важко простежити зв'язок з е.
Одним з моїх найсерйозніших математичних жалю є те, що я ще не вивчив диференціальні рівняння. Але я хочу це зробити, і підозрюю, що правильне розуміння синуса і експоненти зіграють в цьому вирішальну роль.
Підсумуємо
Моєю метою було відокремити синус від тривіальних математичних визначень ( «частина окружності») і надати йому свою власну форму:
- Синус - це плавне, коливальний рух між мінімумом (-1) і максимумом (1). Математично ви прискорюєтеся назад напрямку свого руху. Цей «негативний відсоток» утримує синус від нескінченного зростання.
- Синус зустрічається в колах і трикутниках (а також вібраціях, звукових хвилях, коливаннях маятника і т.д.).
- π - це час, за яке sin (x) проходить від 0 до 0. Він не «належить» колах більше, ніж 0 або 1.
Синус стане одним їх ваших розумових інструментів (Хм, мені потрібна формула для опису плавних змін ...).
У підсумку ми зрозуміємо основи інтуїтивно (е, π, радіани, уявні числа, синус ...) і навчимося змішувати їх в чудовий математичний салат. Смачного!
Переклад статті « Intuitive Understanding of Sine Waves »
Але що вони означають?Прибулець: Невже?
Бачиш отой цегла?
Прибулець: Тобто лінія - це частина фігури?
Розумієш?
Бачите?
Помітили це плавний рух вперед-назад?
Велика різниця - бачите, якими різкими стали руху на краях амплітуди?
Ви по ньому уявляєте, що таке синус?
Бачите, як смайлик рухається вперед-назад?



